Introduction to Computation Models and Optimization Problems
The main topic of the course is Computation Models. How do we use computation to understand the world in which we live
So What is Computation Models?
Computation Models - Experimental devices that help us to understand something that has happened or to predict the future. There are three types of computation models -
Optimization models
Statistical models
Simulation models
What is an Optimization Model?
The notion of an optimization problem provides a structured way to think about solving computational problems. Whenever you set about solving a problem that involves finding the biggest, the smallest, the most, the fewest, the fastest, the least expensive, etc, there's a good chance that you can map that problem onto a classic optimization problem.
So What is an Optimization Model?
An objective function that is to be maximized or minimized.
- Minimize time spent travelling from New Delhi to Mumbai
A set of constraints (possibly empty) that must be honoured:
Cannot spend more than 5000 INR
Must be in Mumbai before 8 PM
A SPECIFIC OPTIMIZATION PROBLEM - KNAPSACK PROBLEM
To understand Knapsack lets take an example of a burglar. So a burglar has to decide what to steal. The problem is that most homes contain more things of value than the average Burglar can carry away.
Suppose a burglar has a knapsack (an old term for backpack as well) that can hold at most 20 pounds of loot breaks into a house and finds the items below, so he needs to decide what to take and what to leave behind.
| ITEMS | VALUE | WEIGHT | VALUE/WEIGHT |
| Clock 🕰️ | 175 | 10 | 17.5 |
| Painting 🖼️ | 90 | 9 | 10 |
| Radio 📻 | 20 | 4 | 5 |
| Vase 🏺 | 50 | 2 | 25 |
| Book 📕 | 10 | 1 | 10 |
| Computer 💻 | 200 | 20 | 10 |
So the thief might choose the best item first , then the next best , and continue until he reached his limit (greedy-algorithm-approach).
But what is best item here ? Is the best item the most valuable , the least heavy , or maybe the item with highest value-to-weight ratio.
Lets get back to Knapsack problem
The basic idea behind a knapsack problem is a simple one :
We have got a knapsack with finite capacity and more objects you'd like to put in than will actually fit in, and you're deciding which objects to take, and which objects to leave behind. Essentially, we have limited strength and there's a maximum weight we can carry. How do we decide what to take and which to leave behind?
There are two variants of the knapsack problem
0/1 Problem
Continuous or fractional problem
So the 0/1 knapsack problem means you either take the object or you don’t. The continuous or fractional knapsack problem says I can take pieces of it.
For example in above burglar example you either take the computer or you don’t. But if there is a a bag full of gold dust you can take pieces from it (for example : half of bag of gold dust)
Let us formalize 0/1 knapsack problem:
Each item is represented by a pair
<value, weight>The knapsack can accomodate items with a total weight of no more than
wA vector
L, of length n represents the set of available items . Each element of vector is an item.A vector, V, of length n , is used to indicate wether or not items are taken . If V[i] = 1, item L[i] is taken. If V[i] = 0, item L[i] is not taken . So I am using a binary number to represent the set of items I chose to take.
Find a V that maximizes
$$\sum^{n-1}_{i=0}V[i]*L[i].value$$
subject to the constraint that
$$\sum^{n-1}_{i=0}V[i]*L[i].weight\leq w$$
The first equation equals the sum of the value of all of the items we decide to take while the second equation says we need to obey the that for all items we take the weight sum up to be less than w.
How to solve these problems:
BRUTE FORCE ALGORITHM :
Enumerate all the possible combination of items i.e, generate all subsets of of set of subjects. This is called power set.
Remove all the combination whose total units exceeds the allowed weight
From the remaining combination choose anyone whose value is largest.
However its usually not very practical since calculating all possibilities will take a lot of time. For example , if there are 100 items to choose from , the power set of size :
1,267,650,600,228,229,401,496,703,205,376.
Solving optimization problems is computationally challenging; hence, a greedy algorithm is often a practical approach to finding a pretty good approximate solution to an optimization problem.
GREEDY ALGORITHM AS A PRACTICAL ALTERNATIVE
while knapsack not full:
put best available item in knapsack
Again we encounter the question what is best? Is the best item most valuable or least in weight? Or is it the highest raitio of value to units?
An Example :
You are about to sit down to a meal and you know how much you value different foods (eg: you like donuts more than apples). But you have a calorie budget (e,g : you don’t want to consume more than 750 calories ). Choosing what to eat is a knapsack problem
So here’s a menu for above example
| FOOD | wine 🍷 | beer 🍺 | pizza 🍕 | burger 🍔 | fries 🍟 | coke 🥤 | apple 🍎 | donut 🍩 |
| Value | 89 | 90 | 30 | 50 | 90 | 79 | 90 | 10 |
| Calories | 123 | 154 | 258 | 354 | 365 | 150 | 95 | 195 |
Lets look at problem that we can use to decide what to order and find a optimal menu.
We will start with an abstract data type
class Food(object):
def __init__(self,n,v,w):
self.name = n
self.value = v
self.calories = w
def getValue(self):
return self.value
def getCost(self):
return self.calories
def density(self):
return self.getValue()/self.getCost()
def __str__(self):
return self.name + ': <' + str(self.value) + ',' + str(self.calories) + '>'
I can initialize things i.e, name of Food , value of Food and calories of a Food under class Food
I have getters for self.value and self.calories , density is going to be the ratio of value and cost and then a string representation.
def buildMenu(names, values, calories):
"""names, values, calories lists of same length.
name a list of strings
values and calories lists of numbers
returns list of Foods"""
menu = []
for i in range(len(values)):
menu.append(Food(names[i], values[i], calories[i]))
return menu
Then I am going to build a function name buildMenu which will take in a list of names and a list of values and a list of calories and it will build the menu.
Now we will implement the greedy algorithm :
#implementation of greedy algorithms
def greedy(items, maxCost, keyFunction):
"""Assumes items a list, maxCost >= 0,
keyFunction maps elements of items to numbers"""
itemsCopy = sorted(items, key = keyFunction,reverse = True)
result = []
totalValue, totalCost = 0.0, 0.0
for i in range(len(itemsCopy)):
if (totalCost + itemsCopy[i].getCost()) <= maxCost:
result.append(itemsCopy[i])
totalCost += itemsCopy[i].getCost()
totalValue += itemsCopy[i].getValue()
return (result, totalValue)
Here keyFunction going to map elements of items to number and I want to sort them from best to worst and this function will tell us whats the best. So maybe keyFunction will just return the value or maybe it will return the weight or maybe it will return the density. But in conclusion I want to use greedy algorithm independently of definition of best and hence I use the keyfunction here.
And then in above for loop , if (totalCost + itemsCopy[i].getCost()) <= maxCost:
(i.e, just the second mathematical equation we described above) and append the best items in result until we can append no more and then I will just return.
But How efficient is above algorithm?
We know sorted() have an time complexity of O(nlogn) and for loop has an time complexity of O(n)
So time complexity of greedy algorithm is
$$O(nlogn) + O(n) = O(nlogn)$$
So its pretty efficient and can be done for set size of millions as well.
So here’s some code that uses greedy
def testGreedy(items, constraint, keyFunction):
taken, val = greedy(items, constraint, keyFunction)
print('Total value of items taken =', val)
for item in taken:
print(' ',item)
It takes in the items , constraints in this case will be maxCost and just calls greedy and prints what result we have.
def testGreedys(foods, maxUnits):
print('Use greedy by value to allocate', maxUnits,
'calories')
testGreedy(foods, maxUnits, Food.getValue)
print('\\nUse greedy by cost to allocate', maxUnits,
'calories')
testGreedy(foods, maxUnits,
lambda x: 1/Food.getCost(x))
print('\\nUse greedy by density to allocate', maxUnits,
'calories')
testGreedy(foods, maxUnits, Food.density)
We call testGreedy here multiple times based on different keyfunctions. But we stumble on something interesting - we have used lambda function above
lambda function
Python supports the creation of anonymous functions (i.e, functions that are not bound to a name), using the reserved word
lambda. The general form lambda expression islambda <sequence of variable names>: <expression>For example
lambda expression x,y : x**yreturns a function that returns thexraised to poweryL = [] for i in map(lambda x,y : x**y, [1,2,3,4] , [3,2,1,0]): L.append(i) print(L) Output: [1,4,3,1]Here in this case
lambda x: 1/Food.getCost(x)lambda is returning the reverse the cost as we want the items with lesser calories.lambda helps to create one liner functions.
Now lets run the code
names = ['wine', 'beer', 'pizza', 'burger', 'fries',
'cola', 'apple', 'donut', 'cake']
values = [89,90,95,100,90,79,50,10]
calories = [123,154,258,354,365,150,95,195]
foods = buildMenu(names, values, calories)
testGreedys(foods, 750)
This is the output we get
Use greedy by value to allocate 750 calories
Total value of items taken = 284.0
burger: <100,354>
pizza: <95,258>
wine: <89,123>
Use greedy by cost to allocate 750 calories
Total value of items taken = 318.0
apple: <50,95>
wine: <89,123>
cola: <79,150>
beer: <90,154>
donut: <10,195>
Use greedy by density to allocate 750 calories
Total value of items taken = 318.0
wine: <89,123>
beer: <90,154>
cola: <79,150>
apple: <50,95>
donut: <10,195>
From this we see an important point of greedy algorithm that we use the algorithm and we got different answers. Why do we have different answers?
The problem is that the greedy algorithm makes a sequence of local optimizations and chooses the locally optimal answer at every point and that doesn’t necessarily add up to a globally optimized answer.
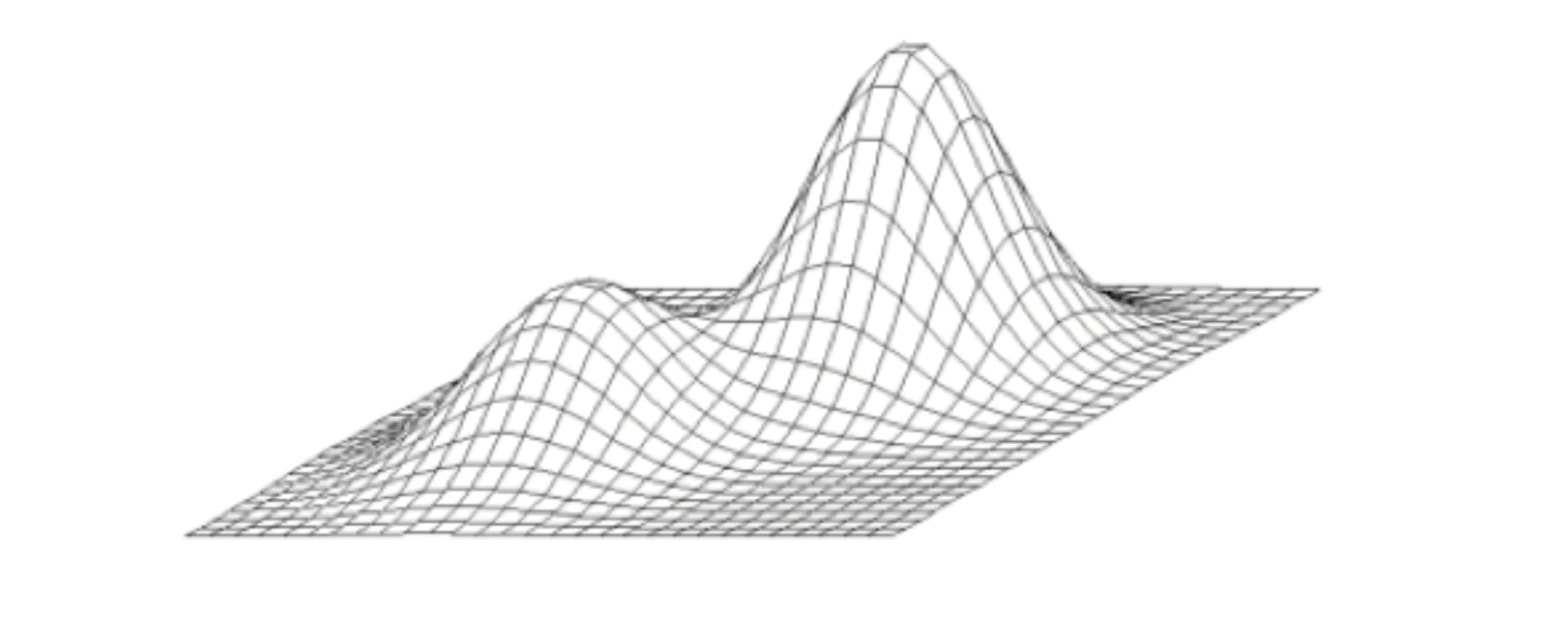
This is often illustrated by showing an example of hill terrain that looks something like above and you want to get to the highest point you can get. So you might choose as a greedy algorithm —> if you can go up go up ; if you can’t go up , you stop. So whenever you get a choice you go up.
Suppose you are between two terrains you can either go left or right , if you go left you will find yourself at local maximum rather than global maximum.
And there is no definition of best sometimes greedy by value will work , sometimes greedy by destiny , sometimes no definition will work. So you can get a good solution with greedy algorithm but you cannot get to a optimial situation with it.
So remember burglar the very first example ? Why don't you apply greedy algorithm to find best solution for the burglar. 😄
Liked this article. Follow me on twitter 🐦